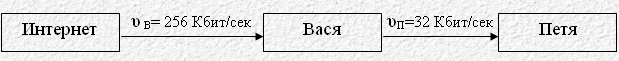ЕГЭ по информатике и ИКТ, прошедший 26 мая 2009 года, сдавало 67430 выпускников из 18 регионов. В итоге: не сдали экзамен 11,4% участников. Максимальную оценку (100 баллов) получили 40 человек. Двое моих учеников получили самый высокий балл по области ‑ 95. Хотелось бы остановиться на некоторых проблемах, связанных с подготовкой к ЕГЭ, и поделиться своим опытом, как с ними легче справиться.

Практика последних лет показала, что источником большинства ошибок являются:

1.     незнание таблицы функции 2^I;

2.     неумение подсчитывать информационный объем;

3.     неумение определять скорость и время передачи информации;

4.     слабая арифметическая подготовка выпускников.

Экзамен проверяет знания и умения выпускников на различных уровнях: базового, повышенного уровня и высокого. Чем меньше времени учащийся потратит на выполнение заданий базового и повышенного уровней, тем успешнее будет его работа в целом. Для этого необходимо обратить внимание на вышеперечисленные ошибки и постараться их избежать.

1. Как запомнить таблицу функций 2^I.

Если первые значения не вызывают затруднения в запоминания, то, начиная со значения 2⁵, ученики начинают путаться. Я постаралась научить запоминать значения, используя следующее:

·        2⁶=64, то есть степень 6 и ответ начинается на цифру 6;

·        2⁵ «привязывается» к 2⁶ , то есть в два раза меньше запомненного числа 64;

·        2⁸ ассоциирует с количеством клавиш клавиатуры и информационным весом для 256 символов;

·        2¹⁰ не вызывает затруднения в запоминании, так как связано с понятием Кбайт, Мбайт и т.д., а к этому значению примыкают 512 и 2048;

·        2¹⁵ напрямую связано с представлением целого числа в машине в 16-битной кодировке, а они уже знают значение максимального числа (32767+1 под ноль), 2¹⁶ «привязываю» к 2¹⁵.

Такое запоминание, освоенное на ассоциациях, быстро усваивается нашей памятью.

2. Подсчет информационного объема текстового сообщения или растрового изображения.

При расчетах количества информации обязательно вначале надо проанализировать условие задачи и записать ее условие в наглядном виде и помнить, в расчетах используются всего 2 формулы:

·         

·        V=K*I,

где:    N – мощность алфавита или количество цветов;

         I – информационный вес символа или глубина цвета;

         V – объем сообщения или объем изображения;

         К – количество символов в сообщении или количество точек в изображении.

Пример 2.1. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1,25 Кбайтов?

Пример 2.2. Для хранения растрового изображения размером 128x128 пикселей отвели 4 килобайта памяти. Каково максимально возможное число цветов в палитре изображения?

Подобные задачи, в условии которых даны большие числа, решаются проще, если выделить в этих числах степени двойки (как это делается в данной задаче).

3. Определение скорость и времени передачи информации.

Пример 3.1. У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 256 Кбит в секунду. Петя получает информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 32 Кбит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 5 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?

Проанализируем условие задачи.

1)   

2) Передаваемый объем Пете V_П=5Мбайт.

3) Начальный объем скаченной Васей информации, после которого начнется передача Пете V_В=512 Кбайт.

4) Искомое время T складывается из времени закачки Васей 512 Кбайт (Т₁) плюс время, которое требуется для приема Петей 5 Мбайт (Т₂): Т=Т₁+Т₂.

Несогласованность единиц измерения может привести к ошибке, поэтому надо требовать от ученика проставлять размерность после каждого полученного промежуточного результата.

4. Представление числовой информации в памяти компьютера, переводы в различные системы счисления.

Как уже говорилось выше, ученики делают много арифметических ошибок и чаще всего при переводе чисел из одной системы счисления в другую. Если осуществлять перевод из 10-ой системы в двоичную, то быстрее это делать так: сначала перевести число в 8-ую, а затем из 8-ой в 2-ю. В этом случае деление столбиком имеет более короткую запись и вероятность совершения ошибки уменьшается. Но для этого надо знать очень хорошо таблицу перевода восьмеричных чисел в двоичную. Для лучшего запоминания таблицы соответствия 8-ых и 16-ных двоичным кодам советую сначала запомнить некоторые числа, а другие «привязать» к ним.

Теперь, если помнить, что 4₈ это 100₂, то 5₈ – это 101₂. Особенно хорошо запомнить, что А₁₆, которая соответствует 10₁₀, в двоичной системе, ‑ это дважды повторенная 10. Запомнить указанные числа, а постепенно и остальные остаются в памяти.